integrál

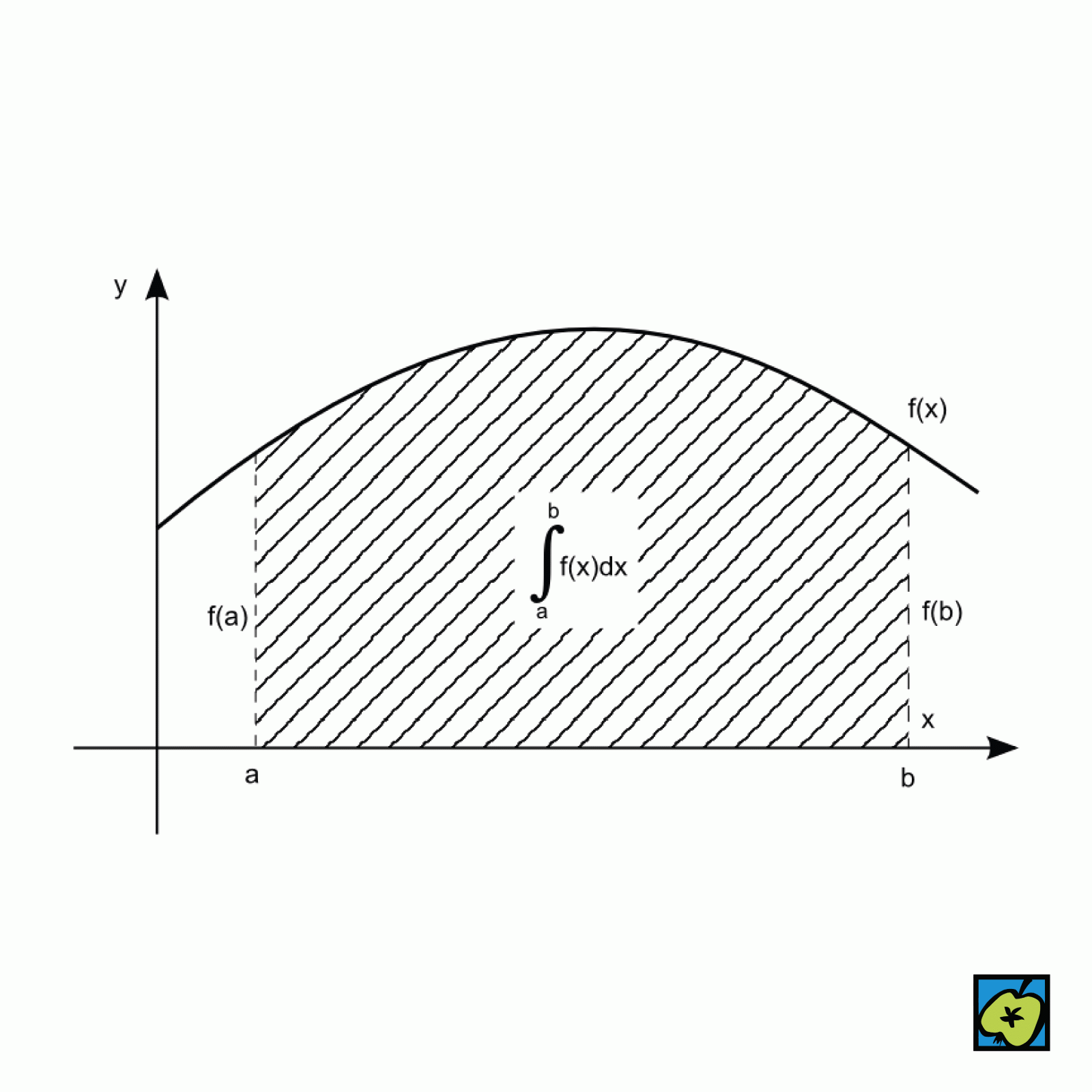
[Latina], jeden ze základních pojmů matematické analýzy. Počátky užívání integrálu jsou u I. Newtona a G. W. Leibnize (17. století). V současné matematice znamená integrál zpravidla určitý integrál. V nejjednodušším případě se definuje integrál funkce \( f \) od \( a \) do \( b \), kde \( f \) (tzv. integrand) je reálná funkce definovaná na intervalu \(\langle a, b \rangle\). Zvolí se taková čísla \( a_0, a_1, \dots, a_k \), že platí \( a = a_0 < a_1 < \dots < a_k = b \) (tzv. dělení intervalu \(\langle a, b \rangle\)), a čísla \( c_1, c_2, \dots, c_k \), že platí \( a_{j-1} \leq c_j \leq a_j \) pro \( j = 1, 2, \dots, k \). Utvoří se tak zvaný integrální součet:

\[ S = \sum_{j=1}^{k} f(c_j)(a_j - a_{j-1}). \]

Jestliže při neomezeném „zjemňování“ dělení (tj. zvětšování počtu dělících bodů \( a_j \) a zkracování vzdáleností \( a_j - a_{j-1} \)) se integrální součty \( S \) blíží jisté pevné hodnotě, nazýváme toto číslo integrálem funkce \( f \) od \( a \) do \( b \) a označujeme:

\[ \int_a^b f(x)\,dx. \]

(To je tzv. definice Riemannova integrálu.) V geometrii \(\int_a^b f(x)\,dx\) představuje obsah části roviny ohraničené osou \( x \), grafem funkce \( f \) a úsečkami rovnoběžnými s osou \( y \) ve vzdálenostech \( a \) a \( b \). Pokud je některá část obrazce pod osou \( x \), bere se její obsah se záporným znaménkem. Název neurčitý integrál se dříve užíval pro označení primitivní funkce. Vztah mezi určitým integrálem a primitivní funkcí udává vzorec (kde \( F \) je libovolná primitivní funkce k \( f \) na \(\langle a, b \rangle\)):

\[ \int_a^y f(x)\,dx = F(y) - F(a), \quad y \in \langle a, b \rangle. \]

Tento vzorec použil k definici integrálu I. Newton. Ukazuje, že pojem integrál je v jistém smyslu protikladem pojmu derivace. Popsaný integrál funkce jedné proměnné se někdy nazývá jednoduchý integrál. Obdobným způsobem pomocí integrálních součtů lze definovat integrál funkcí více proměnných (např. dvojný, trojný či n-rozměrný integrál), a rovněž křivkový a plošný integrál. Vícenásobný integrál vzniká postupným integrováním podle jednotlivých proměnných a značí se např.:

\[ \int_c^d \int_a^b f(x, y)\,dx\,dy \]

pro dvojný integrál funkce \( f(x, y) \), kde \( a \leq x \leq b \) a \( c \leq y \leq d \). Obecný vícerozměrný integrál funkce \( f \) přes množinu \( P \) se pak zapisuje jako:

\[ \iint_P f(x, y)\,dx\,dy. \]

Při výpočtu se vícerozměrné integrály převádějí na vícenásobné. Moderní matematika vytvořila řadu zobecnění a modifikací původního pojmu integrál, které se liší rozsahem funkcí, pro něž integrál existuje, i konkrétními vlastnostmi. Umožňují stanovit integrál i přes složitější množiny než intervaly. K nejdůležitějším patří Lebesgueův–Stieltjesův integrál a Perronův integrál. Pojem integrál je důležitý v řadě aplikací – používá se při výpočtu délek křivek, obsahů, objemů, hmotnosti, práce, potenciálu aj. Odvětví matematiky, které se zabývá výpočtem integrálů, se nazývá integrální počet. Ten zkoumá zejména metody nalezení primitivní funkce k dané funkci, což umožňuje výpočet integrálu podle Newtonova vzorce, ale zahrnuje i numerické metody.