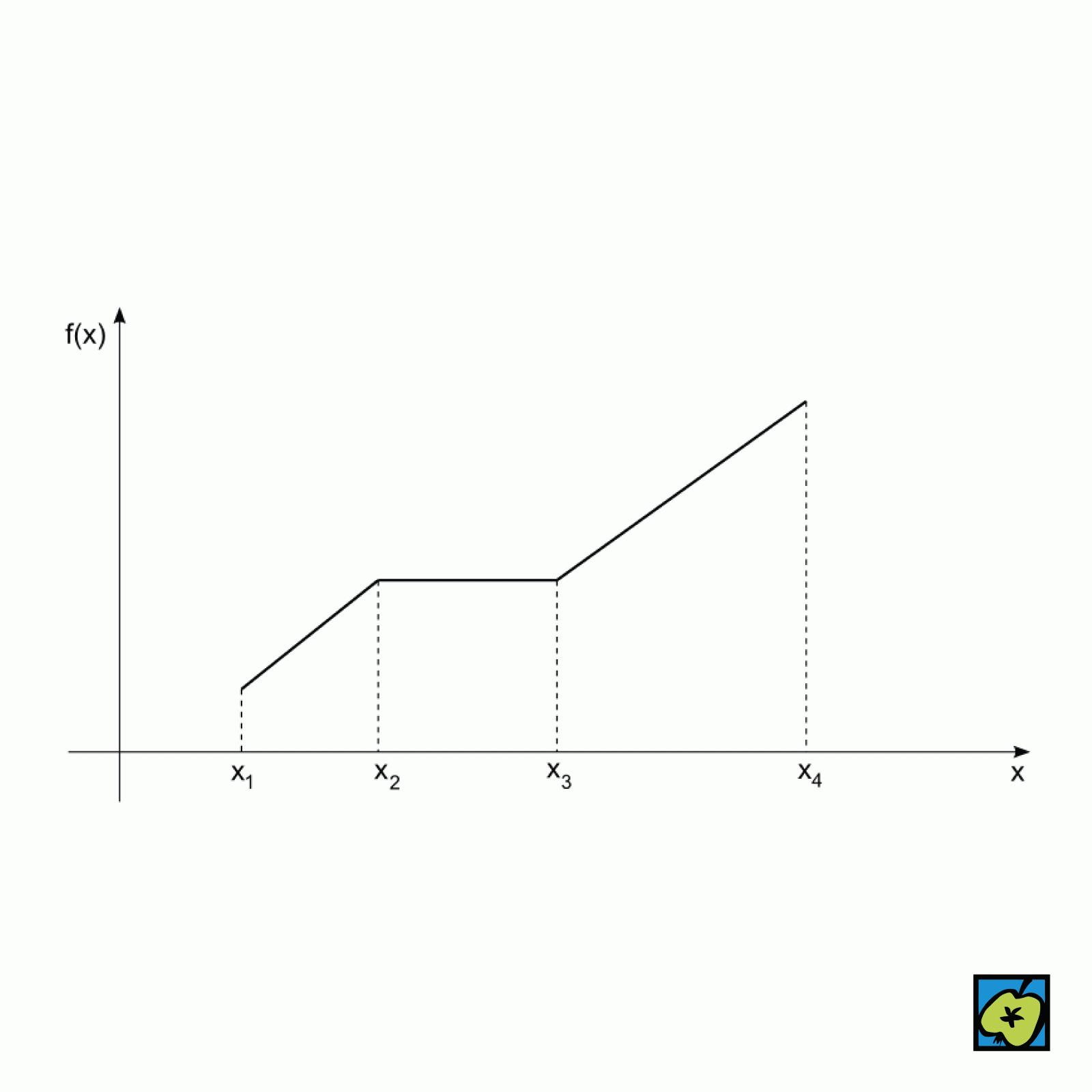
monotónní funkce

Monotónní funkce v množině B je reálná funkce reálné proměnné, tj. \(\mathcal{f}\) : \(A→R\), \(A⊂R\), která v množině \(B ⊂A\) splňuje jednu z podmínek:

1. \(\mathcal{f}(x_1) \leq \mathcal{f}(x_2)\), jakmile je \( x_1, x_2 \in B, x_1 < x_2\) ,

2. \(\mathcal{f}(x_1) \geq \mathcal{f}(x_2)\), jakmile je \( x_1, x_2 \in B, x_1 < x_2\) .

Splňuje-li funkce \(\mathcal{f}\) dokonce jednu z podmínek

3. \(\mathcal{f}(x_1) < \mathcal{f}(x_2)\), jakmile je \( x_1, x_2 \in B, x_1 < x_2\) ,

4. \(\mathcal{f}(x_1) > \mathcal{f}(x_2)\), jakmile je \( x_1, x_2 \in B, x_1 < x_2\) ,

pak se nazývá ryze monotónní v množině B. Platí-li 1., pak funkce \(\mathcal{f}\) se nazývá neklesající v B. Platí-li 2., pak funkce \(\mathcal{f}\)  se nazývá nerostoucí v B. Platí-li 3., pak funkce \(\mathcal{f}\) se nazývá rostoucí v B. Platí-li 4., pak funkce \(\mathcal{f}\) se nazývá klesající v B. Je-li \(B=A\), potom lze stručněji říci, že funkce \(\mathcal{f}\) je monotónní; platí-li při tom 3. nebo 4., říká se, že funkce f je ryze monotónní.